方程式と関数の違い

人気の比較

主な違い：数学では、式は2つの式の間の等価性を表すために使用されます。一方、関数は方程式よりもはるかに複雑です。関数は、一組の入力と一組の対応する出力との間の関係を示すために使用される。

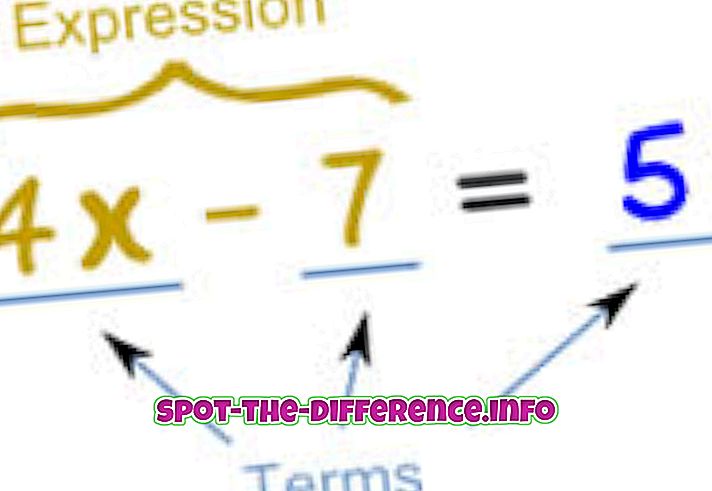
方程式と関数は、数学の主題である代数の2つの基本的な基礎です。どちらも本質的に非常に複雑になることがありますが、その基本的な形式では、それらは互いに混同される可能性があります。方程式と関数の主な違いは、方程式は通常単一の入力を扱うのに対し、関数は多数の入力を持つことができるという事実です。

数学では、式は2つの式の間の等価性を表すために使用されます。基本的に、式は式が別の式と等しいと書かれています。例：x + 2 = 5これは、xに2を加えた場合、xが2であれば5に等しいことを意味します。したがって、xの方程式3は2 + 3 = 5として解くことができます。

方程式はそれよりも複雑になる可能性があり、x、y、zなどのような複数の変数を単一の方程式に含めることができます。例：3x + 2y - z =4。ただし、各アルファベットは1つの数字に対応します。この場合、ｘ＝１、ｙ＝２、ｚ＝３である。

したがって、

3x + 2y - z = 4

3（1）+ 2（2） - 3 = 4これは

3 + 4 - 3 = 4本質的に

4 = 4

一方、関数は方程式よりもはるかに複雑です。関数は、一組の入力と一組の対応する出力との間の関係を示すために使用される。基本的に、入力は単一の出力を与えます。関数は2つの変数間の関係です。例えば：f（x）= x + 2.この関数によれば、入力が何であれ、それはあなたに単一の出力を与え、それは入力に2を加えたものになります。この関数を解いてみましょう：

入力	関数	出力
バツ	f（x）= x + 2	f（x）
1	1 + 2	3
2	2 + 2	4
3	3 + 2	5
4	4 + 2	6
5	5 + 2	7

等々…

関数は、数学、物理学、コンピュータサイエンスなどでさまざまな用途があります。それらは、上に示したような単純な関数から複雑な式やアルゴリズムまで、さまざまです。関数は入力に対して出力を与える機械と考えることができ、その出力は何らかの形で入力に関連しています。

関数は常に3つの部分、入力、関係、そして出力を持ちます。関数を書くための古典的な方法は "f（x）= ..."です。ここでxは入力を表し、f（x）は出力を表します。

上述したように、方程式と関数の主な違いは、方程式は通常、式が等しくなるようにする入力が1つだけであるということです。一方、関数にはさまざまな入力があり、それぞれ入力が出力されます。

推奨されます

古ダイエットと地中海ダイエットの違い

主な違い：パレオダイエットと地中海ダイエットは、最近非常に人気がある2種類のダイエットです。古ダイエットは旧石器時代の食事療法の略です。それは先史時代の人が続いていた食事療法の利点を宣伝しています。地中海ダイエットは地中海周辺地域、特にギリシャ、南イタリア、そしてスペインの食事パターンの組み合わせに従います。産業革命以来、座りがちな生活様式はゆっくりだが着実に増えてきました。以前は、人々は畑で働いたり、市場に何時間も歩いたりする傾向がありました。今では、技術的な利点により、誰もそのようなことをする必要はありません。その代わりに、私たちは一日中スクリーンの前の椅子に座ることによって生計を立てます。工業時代と技術時代は多くの改善をもたらしましたが、それは私たちの体力に悪影響を及ぼしました。フィットネス活動の欠如は肥満の増加をもたらしました。実際、一部の先進国では人口の半分以上が過体重です。人々が健康と体重についてより意識するようになるにつれて、彼らは彼らの体重を維持するために食事療法に目を向け始めました。古ダイエットと地中海ダイエットは、最近非常に人気がある2種類のダイエットです。多くの人々はこれらの食事療法を流行として批判しています、それは彼らが不均衡な栄養摂取をもたらす特定の種類の食物摂取を制限することを意味します。流行食は通常短期間の体重減少につながり、

との差
乾電池と乾電池の違い

主な違い：乾電池は乾電池より早く使用できます。湿電池と乾電池の主な違いは、湿電池は液体電解質を使用するのに対し、乾電池はペースト電解質を使用することです。バッテリーは便利なアイテムで、最近も必要なものです。ほとんどすべての機器は、直接電力で動作するか、またはバッテリを使用して電力を蓄えるかのいずれかであり、携帯性も確保しながら機能します。つまり、電源に接続せずにある場所から別の場所に移動できます。乾電池と乾電池の2種類があります。乾電池と乾電池です。「浸水式バッテリー」とも呼ばれるウェットセルバッテリーは、乾電池よりも前のものです。乾電池が有効になり普及する前に主に使用されていました。湿式電池は今日でも使用されていますが、スマートフォンやその他の電子機器から懐中電灯や時計などの通常の家庭用品まで、現在ほとんどすべてに使用されている乾電池よりも一般的ではありません。湿電池と乾電池の主な違いは、湿電池は液体電解質を使用するのに対し、乾電池はペースト電解質を使用することです。電解質は電池がノード間で電荷を移動させるものである。液体電解質を使用するため、湿式電池は特定の向き、すなわち正しい向きで使用する必要があります。それ以外の方法で使用すると、液体電解質がこぼれます。乾電池はこの問題を抱えておらず、一般的にあらゆる方向に使用することができる。

との差
EPOとPPOの違い

主な違い： EPOとPPOは本質的に2種類の医療保険です。 EPOはExclusiveプロバイダ組織を表し、PPOは優先プロバイダ組織です。 PPOは、計画のプロバイダーネットワークの内外で提供されるケアをカバーします。 EPOはプロバイダーネットワークによって提供されるケアのみをカバーします。 EPOとPPOは本質的に2つの異なるタイプの医療保険です。米国では、医療費は非常に高くなっています。したがって、医療費を支払うことはほとんどの市民にとって困難な作業です。これは健康保険が役立つところです。健康保険は、医療費を支払わなければならないリスクから保護する一種の保険です。健康保険では、被保険者は毎年保険料を支払い、保険会社は補償期間内に保険金が発生した場合にはいつでも保険料を支払います。ただし、これらの健康保険は、他のすべての保険と同様に、特定の契約条件に従います。たとえば、保険は特定の種類の病気、提供された特定の種類の医療、または特定の病院のみを対象とすることがあります。また、保険会社はすべての医療費を全額支払うことも、支払うべき金額の一部だけを支払うこともできます。一般に利用可能な健康保険には、HMO、PPO、EPO、POSの4つの主な種類があります。 HMOは健康管理組織、PPOは優先プロバイダ組織、EPOは独占プロバイダ組織を表し、POSはポイントオブサービ

との差
祭壇と祭壇の違い

主な違い：祭壇はほとんどの宗教で共通の構造です。それはテーブルまたは平らな面であり、その上に供物や犠牲がなされます。一方、Alterは変化を表す動詞です。 alterの公式な定義では、「変更することまたは異なるものにすること」と述べています。 AltarとAlterという2つの単語は似ているように見えますが、実際にはまったく異なる2つのことを示しています。実際、AltarとAlterは、1文字のスペルが異なることを除けば、遠くには似ていません。これは、彼らが混乱する主な理由でもあります。実用的には、祭壇は宗教的な構造ですが、alterは変化を表す動詞です。祭壇はほとんどの宗教で共通の構造です。それはテーブルまたは平らな面であり、その上に供物や犠牲がなされます。宗教によっては、これらの供え物や犠牲は神あるいは宇宙そのものになされることができます。祭壇は神社、寺院、教会、その他の礼拝所にもあります。祭壇は、古代や異教の宗教でもよく使われていました。今日では、キリスト教、仏教、ヒンズー教、神道、道教、そして新異教主義や儀式用マジックで今でも使われています。一方、Alterは変化を表す動詞です。 alterの公式な定義では、「変更または異なるものにする」ことが述べられています。それは、通常はより良い方向に変更する必要があるが、必ずしもそうではないことを示しています

との差
マスタードオイルと植物油の違い

主な違い：一般に、植物油はさまざまな植物とその原料から得られます。このカテゴリにはマスタードシードから得られるマスタードオイルも含まれます。今日では、油は多くの成分の代替品として使用されており、料理や薬用としても使用されています。工業用に油も大量に使用されています。ほとんどの油がバイオディーゼルの原料になりました。精製油、未精製油、原油など、さまざまな種類の油とその種類があります。これらはそれぞれ異なる分野でそれぞれの用途があります。油中の脂肪およびコレステロール含有量は、これらの成分が健康に関連する多くの問題および問題の原因であるため、調理および他の関連用途に使用する場合には考慮する必要があります。植物油は、種子、ハーブ、ナッツ、マメ科植物および果物のような様々な植物および供給源から得られる様々な種類の油を含む。植物油は植物から抽出されたトリグリセリドです。「植物油」という用語は、具体的には室温で液体である物質を指すか、または一般に、所与の温度での物質の物質の状態も指す。それ故、これらは室温で固体でありそして通常の他の油と同様に加熱すると液化する。実際にはこれらの油はあらゆる植物源から得られるが、商業ベースでは、油は一般に種子から抽出される。植物油の最も一般的な品種には、オリーブ油、大豆油、コーン油、ベニバナ油、およびピーナッツ油が含まれます。植物油は、

との差
DSPと汎用プロセッサの違い

主な違い：マイクロプロセッサは、単一または少数の集積回路上にコンピュータの中央処理装置（CPU）の機能を組み込んでいます。マイクロプロセッサの目的は、デジタルデータを入力として受け取り、それを命令に従って処理してから出力することです。ほとんどの汎用マイクロプロセッサはパーソナルコンピュータに存在します。それらは多くの場合、計算、テキスト編集、マルチメディア表示、およびネットワークを介した通信に使用されます。他方、ＤＳＰプロセッサは特定のタイプのマイクロプロセッサである。 DSPはデジタル信号処理を表します。基本的にはデジタル信号または情報信号に対して行われる信号処理です。マイクロプロセッサは、単一または少数の集積回路上にコンピュータの中央処理装置（ＣＰＵ）の機能を組み込んでいる。マイクロプロセッサの目的は、デジタルデータを入力として受け取り、それを命令に従って処理してから出力することです。これはシーケンシャルデジタルロジックとして知られています。マイクロプロセッサは内部メモリを持ち、基本的にバイナリシステムで動作します。汎用マイクロプロセッサとは、特定の言語またはソフトウェアに結び付けられていないか、それらと統合されていないプロセッサです。ほとんどの汎用マイクロプロセッサはパーソナルコンピュータに存在します。それらは多くの場合、計算、テキスト編集、マルチメデ

との差
DSPプロセッサとマイクロコントローラの違い

主な違い： DSPはデジタル信号処理の略です。基本的にはデジタル信号または情報信号に対して行われる信号処理です。 DSPプロセッサは、デジタル信号処理の運用上のニーズに合わせて最適化されたアーキテクチャを持つ特殊なマイクロプロセッサです。一方、マイクロコントローラは、プロセッサコア、メモリ、およびプログラム可能な入出力ペリフェラルを含む単一の集積回路上の小型コンピュータです。マイクロコントローラはしばしばプログラムメモリと少量のＲＡＭも含む。マイクロコントローラとDSPプロセッサは、2種類のマイクロプロセッサです。それらは、ユーザによって与えられるように特定のアプリケーションまたはタスクを実行するようにプログラムされています。どちらもデバイス上のバイナリデータを操作することによって動作します。ただし、両者は性質がまったく異なります。 DSPはデジタル信号処理を表します。基本的にはデジタル信号または情報信号に対して行われる信号処理です。 DSPは信号を修正または改善することを目的としています。これは、離散時間、離散周波数、離散ドメイン信号などの離散単位の表現によって特徴付けられます。ＤＳＰは、通信信号処理、レーダ信号処理、センサアレイ処理、デジタル画像処理などのようなサブフィールドを含む。 DSPプロセッサは、デジタル信号処理の運用上のニーズに合わせて最適化されたア

との差
吸熱と恒温の違い

主な違い：吸熱は、外部の周囲の熱の助けを借りずに体温を好ましい程度に維持する有機体です。吸熱は、内部プロセスによって放出される熱を使用または放出することによってこれを行います。恒温は、外的影響にかかわらず安定した体内温度を維持するために使用される体温調節のプロセスであるため、恒温は実際には吸熱と密接に関係しています。吸熱は実際に彼らの内部体温を制御下に保つために恒温のプロセスを使用します。吸熱と恒温の用語は、その類似性のためにしばしば混乱しやすい用語です。これらの用語は関連しており、それらの内部機能を制御するためにそれらの身体機能を自動的に変えることができる有機体を指します。私たちの体は温度を上げるために震え、体から余分な熱を放出するために汗をかくように人間は吸熱です。体は恒常性を維持するために外部の温度に応じて自動的に機能を変えるので、それは非常に興味深い概念です。吸熱は、外部の周囲熱の助けを借りずに体温を好ましい程度に維持する有機体です。吸熱は、内部プロセスによって放出される熱を使用または放出することによってこれを行います。あるタイプのエネルギーが別のエネルギーに変換される瞬間にそれが熱を放出することは常識です。状態を変えているエネルギーでさえも熱を放出します。外が暑い日には、体は熱を放出して内部の温度を維持します。寒い日に、体は熱を消費し、より多くの

との差
ソニーのXperia ZとiPhone 5の違い

主な違い：ソニーのXperia Zは、ソニーモバイルによって設計、製造、販売されている最新のスマートフォンで、2013年2月に発売されました。シャープでクリアな表示この携帯電話は、1.5 GHzのクアッドコアKrait、最大16 GBの内部メモリ記憶容量と最大32 GBの拡張可能な記憶容量を持つ2 GBのRAMを搭載しています。 iPhone 5はアップル社の最新の革新的な製品です。彼らはさらにいっそういっぱいの機能で新しい電話をよりスリムにして、より薄くそしてより軽くした。 iPhone 5は、640 x 1136ピクセル、1600万色の4インチLEDバックライト付きIPS LCDスクリーンをサポートしています。この電話機には、コーニングゴリラクラスのほか、フロントスクリーンに指紋が入らないようにするための疎油性コーティングなどの安全機能も備わっています。 iPhone 5には、6.1にアップグレード可能な最新のApple iOS 6が付属しています。それは1.2 GHzデュアルコアApple A6プロセッサ、PowerVR SGX 543 MP 3と1 GBのRAMを含みます。市場はさまざまな機能とさまざまな技術を提供するさまざまな携帯電話でいっぱいです。スマートフォンは、外出先でも自分の生活を送れるようにするために、多くの人々の生活様式になっています。彼らは映画

との差

エディターズチョイス

NAFTAとEUの違い

主な違い： NAFTAは北米の三国間のルールベースの貿易圏で、3人のメンバーがいます。欧州連合は、主にヨーロッパに居住する28カ国間の政治経済協定です。 NAFTAとEUは、世界中でよく知られている貿易圏です。北米自由貿易協会としても知られるNAFTAは、メキシコ、カナダ、アメリカの3カ国の間の合意です。しかし、EUまたは欧州連合はヨーロッパの20カ国の間で署名された条約です。彼らは貿易圏であるという主な目的を果たしていますが、それらには多くの違いがあります。 NAFTAは、1994年1月1日に発効した、北米における三国間の規則に基づく貿易ブロックです。これは、米国とカナダの間の貿易協定に取って代わるものでした。北米環境協力協定（NAAEC）と北米労働協力協定（NAALC）の2つの補足があります。 NAFTAの主な目的は、米国、カナダ、メキシコ間の貿易と投資に対する障壁を取り除くことです。さらに、関税以外の貿易障壁を排除し、製品の知的財産権を保護することも目的としています。 2つの先進国と1つの発展途上国の間で合意がなされたため、環境と農業の問題は複数の論争を引き起こしました。農業では、各当事者間で3つの別々の契約が締結されました。日米協定には農産物（主に砂糖、乳製品、家禽製品）に対する重大な制限と関税割当が含まれていますが、メキシコと米国の協定では廃止期間の枠内でよ