BツリーとB +ツリーの違い

人気の比較

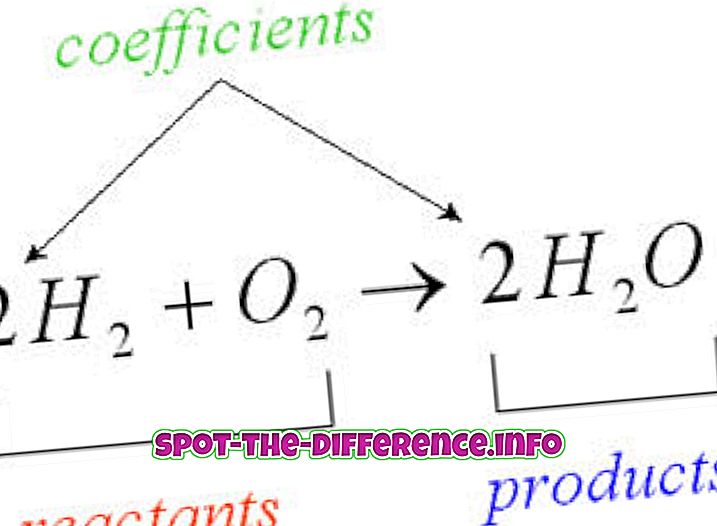
主な違い：コンピュータでは、バイナリツリーはデータを格納し、ユーザーがアルゴリズム時にデータにアクセス、検索、挿入、削除できるようにするツリーデータ構造です。 BツリーとB +ツリーの違いは、Bツリーではキーとデータを内部ノードとリーフノードの両方に格納できるのに対し、B +ツリーではデータとキーはリーフノードにしか格納できないことです。。

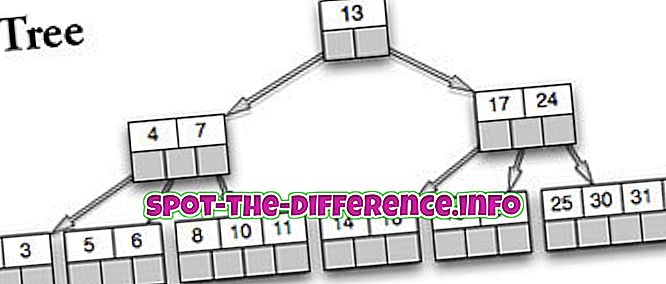
二分木は、磁気ディスクなどの直接アクセス二次記憶装置上でうまく機能するように設計されたバランスのとれた探索木である。 Rudolf BayerとEd McCreightはBツリーの概念を発明しました。

Bツリーは一般化された二分探索木で、どのノードにも3つ以上の子を持つことができます。 Bツリーの各内部ノードには、いくつかのキーが含まれています。これらのキーは値を分離し、さらにサブツリーを形成します。 Bツリーの内部ノードは、事前定義された範囲内に配置された可変数の子ノードを持つことができます。それぞれのノードからデータが挿入または削除されると、子ノードの数が変化します。事前定義された範囲を維持するために、内部ノードを結合または分割することができます。 Bツリーでは、事前定義された範囲を維持する必要があるため、ある範囲の子ノードが許可されます。

Bツリーは、他の自己均衡検索ツリーとは異なり、頻繁にリバランスする必要はありません。これらのツリーのノードは常にいっぱいではありません。したがって、これらの木ではスペースが不要に消費され、スペースが無駄になります。子ノードの数の下限と上限のみが通常、特定の実装に対して固定されています。たとえば、2-3 Bツリー（多くの場合、単に2-3ツリーと呼ばれる）では、各内部ノードに含まれる子ノードは2つまたは3つだけです。

さらに、Bツリーは、大きなデータブロックを読み書きするシステムに最適化されています。データベースやファイルシステムでよく使われています。 Bツリーでは、すべてのノードがルートノードから同じバランスの深さに保たれます。これらの深さは、要素数が増えるにつれてゆっくりと増加します。これにより、すべてのリーフノードがルートからさらに離れたもう1つのノードになります。さらに、Ｂツリーは、データにアクセスするのにかかる時間に関して、他の実施形態と比較したときにより有利である。

B +ツリーはノードを持つn配列ツリーで、ノードごとに多数の子で構成されています。ルートは、リーフまたは3つ以上の子を含むノードです。 B +ツリーは、ルート、内部ノード、およびリーフで構成されています。

B +ツリーはBツリーと同じです。唯一の違いは、B +ツリーの下部にリンクされたリーフが追加された追加のレベルがあることです。また、Bツリーとは異なり、B +ツリーの各ノードにはキーのみが含まれ、キーと値のペアは含まれません。

さらに、バランス係数またはB +ツリーの次数は、ツリー内の内部ノードの容量、つまりそれらが持つことができるノードの数を測定します。ノードに対する実際の子の数は、内部ノードに対して制限されています。ただし、ルートは2つ以上の子を持つことが許可されているため例外です。たとえば、B +ツリーの順序が7の場合、各内部ノード（ルートを除く）は4から7個の子を持つことができます。 B +ツリーの主な価値は、効率的な検索のためにデータをブロック指向のストレージコンテキスト、特にファイルシステムに格納することにあります。

B +ツリーの主な価値はデータの保存と維持にあり、データが失われることはありません。このアプローチは、特にブロック指向のストレージコンテキストと特定のファイルシステムに適用されます。 B +ツリーの一番下のインデックスブロックである葉は、リンクリストで互いにリンクされていることがよくあります。したがって、これにより、ブロックを介した範囲照会または順序付き反復がより単純で効率的になります。さらに、B +ツリーでは占積率が無駄になりません。 B +ツリーは、効率的な住宅データ構造フォーマットを提供します。これにより、アクセスと格納が簡単になります。 B +ツリーは、データが通常ディスクに存在するデータベースシステムインデックスとして特に役立ちます。

BツリーとB +ツリーの比較

	Bの木	B +ツリー
短いウェブの説明	ABツリーは、すべての端末ノードがベースから同じ距離にあり、すべての非端末ノードがnから2 nの間のサブツリーまたはポインタを持つツリー形式の情報格納および検索のための組織構造です。 nは整数です。	B +ツリーは、変数を持つn配列ツリーですが、多くの場合、ノードごとに多数の子を持ちます。 B +ツリーは、ルート、内部ノード、およびリーフで構成されています。ルートはリーフまたは2つ以上の子を持つノードのいずれかです。
としても知られている	バランスのとれた木。	Bプラス木。
スペース	に）	に）
サーチ	O（log n）	O（log _b n）
インサート	O（log n）	O（log _b n）
削除する	O（log n）	O（log _b n）
ストレージ	Bツリーで、内部ノードまたはリーフノードに格納されている検索キーとデータ。	B +ツリーでは、データはリーフノードにのみ格納されます。
データ	3つのストアのリーフノードは、実際のレコードではなくレコードを指します。	ツリーのリーフノードには、レコードへのポインタではなく実際のレコードが格納されています。
スペース	これらの木はスペースを無駄にする	そこの木はスペースを無駄にしません。
葉ノードの機能	Bツリーでは、リーフノードはリンクリストを使用して格納できません。	B +ツリーでは、リーフノードデータは順次リンクリストに並べられます。
検索中	この場合、リーフノードにデータが見つからないため、Bツリーでの検索は困難になります。	ここでは、すべてのデータがリーフノードにあるため、B +ツリー内の任意のデータの検索は非常に簡単です。
検索機能	このBツリーでは、検索はB +ツリーと比べてそれほど簡単ではありません。	ここでB +ツリーでは検索が簡単になります。
冗長鍵	それらは冗長な検索キーを格納しません。	それらは冗長な検索キーを格納します。
アプリケーション	それらは古いバージョンであり、B +ツリーと比べてそれほど有利ではありません。	多くのデータベースシステムの実装者は、B +ツリーの構造上の単純さを好みます。

推奨されます

化学反応と核反応の違い

主な違い：化学反応は、元素の原子が自分自身を再配置して新しい物質を形成するプロセスです。核反応は、原子の核の構造がエネルギーの放出と共に変化する過程である。核反応と化学反応の主な違いは、「原子内での反応のしくみ」から理解できます。核反応は原子の核内で起こります。一方、原子内の電子は化学反応の原因となります。化学反応は、元素をまったく新しい元素に変換するプロセスです。反応開始時の元素は反応物として知られており、反応後に形成された新しい元素は生成物として知られている。１つ以上の反応物が生成物に変換されると、それらは多くの修飾およびエネルギー変化を受ける。化学反応は電子の損失、獲得および共有を含む。元素間のこの電子の移動は化学反応として知られている。化学方程式を使って記述することもできます。触媒、温度、溶媒効果などの方程式を制御するさまざまな要因があります。熱力学の研究を通して、反応を制御することができます。反応速度は単に反応速度を決定します。それは、どの反応、どのくらい遅いか速いかを研究するパラメータです。例を挙げて反応物AとBが生成物CとDに入る次の反応を考えてみましょう。 a A + b B→c C + d D 反応速度は、２つの反応物または生成物のいずれかに関して与えることができる。レート＝ −１／ａ×ｄ［Ａ］／ｄｔ＝ −１／ｂ×ｄ

人気の比較
一眼レフカメラとデジタル一眼レフカメラの違い

主な違い：一眼レフカメラは自動ムービングミラーシステムを備えており、それを通して特定の画像を撮影することができます。移動鏡は、鏡に当たる光を操作し、操作し、そして制御する。 DSLRは、Digital Single-Lens Reflexの略で、デジタルカメラの高度な形式です。一眼レフの略で、一眼レフとは、移動する鏡を使って特定の画像を撮影できるカメラです。移動鏡システムは、鏡に当たる光を操作し、操作し、そして制御する。それは1/500秒以上の驚くべきシャッタースピードを持っています。一眼レフカメラは非常に大きくなる傾向があり、そのレンズは移動可能です。レンズも自分の好みに応じて変更することができます。一眼レフカメラから画像をキャプチャするには、体がはるかに大きいため、多くのスペースが必要です。基本的に、それは一眼レフカメラですべての重要な役割を果たすレンズです。一眼レフカメラはおそらく滑らかでクリーミーな背景を作成します。 5D、60D、100Dはカメラに装着されているレンズタイプで、それを通して画像の品質を向上させることができます。 DSLRは、Digital Single-Lens Reflexの略で、デジタルカメラの高度な形式です。彼らは一眼レフのほとんどの機能を持っていますが、とにかく、彼らはより優れており、高度に開発されています。 DSLRはSLRよ

人気の比較
赤道と主子午線の違い

主な違い：赤道は、北半球と南半球の間に線を引く仮想円です。緯度が計算される場所からのポイントです。つまり、赤道は緯度0°です。主子午線は、地球の地球上で0度の経度測定をマークし、水平方向の緯度線と交差する垂直線です。赤道という用語はラテン語の句、「昼夜を問わず円を平準化する」を意味する「circulus aequator diei et noctis」から派生しています。赤道は、北半球と南半球を結ぶ仮想円です。緯度が計算される場所からのポイントです。つまり、赤道は緯度0°です。それは実際には地球の回転軸との関係に基づいている、主要な架空の緯度円の1つです。簡単に言えば、赤道は仮想の円であり、球の地球を正確に真ん中、つまり2つに分割します。緯度0°（赤道）では、一日の長さは約12時間になります。赤道上の部分は、一年中一定の12時間の日照があります。主子午線という用語は、北極から南極への仮想線で、水平線と交差する垂直線を引きます。それは基本的に地球を二つの半球、すなわち東半球と西半球に分割します。定義された主子午線からの東と西からの方向を使うので、それはそれから2つの半球と呼ばれます。 1884年、国際会議で主子午線が経度0度として正式に設立されました。グリニッジは22人の賛成票、ハイチ人に1人、および2人の棄権者（フランスとブラジル）に選ばれ、子午線に選

人気の比較
方程式と関数の違い

主な違い：数学では、式は2つの式の間の等価性を表すために使用されます。一方、関数は方程式よりもはるかに複雑です。関数は、一組の入力と一組の対応する出力との間の関係を示すために使用される。方程式と関数は、数学の主題である代数の2つの基本的な基礎です。どちらも本質的に非常に複雑になることがありますが、その基本的な形式では、それらは互いに混同される可能性があります。方程式と関数の主な違いは、方程式は通常単一の入力を扱うのに対し、関数は多数の入力を持つことができるという事実です。数学では、式は2つの式の間の等価性を表すために使用されます。基本的に、式は式が別の式と等しいと書かれています。例：x + 2 = 5これは、xに2を加えた場合、xが2であれば5に等しいことを意味します。したがって、xの方程式3は2 + 3 = 5として解くことができます。方程式はそれよりも複雑になる可能性があり、x、y、zなどのような複数の変数を単一の方程式に含めることができます。例：3x + 2y - z =4。ただし、各アルファベットは1つの数字に対応します。この場合、ｘ＝１、ｙ＝２、ｚ＝３である。したがって、 3x + 2y - z = 4 3（1）+ 2（2） - 3 = 4これは 3 + 4 - 3 = 4本質的に 4 = 4 一方、関数は方程式よりもはるかに複雑です。

人気の比較
機械と装置の違い

主な違い：機械的には、機器の設計には機器が必要です。機械はあらゆるタスクを実行するために使用されるツールですが、機器は特定の目的に必要なツールのセットです。「machine」という単語は、ラテン語の「machina」から派生しています。現代の単語の意味は、軍用の攻城兵器への特殊な用途によって影響を受けます。それらは劇場で使用されているステージエンジンでも使用されています。「単純な機械」という発想は、機械、レバー、プーリー、ネジを研究し、レバーの機械的優位性の原理を発見したギリシャの哲学者アルキメデスによって生まれました。さらに、ギリシャの哲学者たちは古典的な5つの単純な機械を定義し、それは機械的な利点を大まかに計算するために使用されていました。彼の研究で、アレクサンドリアのヘロンは、5つのメカニズムをレバー、ウインドラス、プーリー、ウェッジ、そしてネジとして挙げました。そして、それらは動きに負荷をかけることが知られていました。フランダースのエンジニアSimon Stevin は、単純な機械と統合された傾斜面の機械的利点を導き出しました。 Leonardo da Vinci は、滑り摩擦の古典的な規則を発見することによって、機械の研究にも貢献しました。単純な機械は、力の方向または大きさを単純に変換する装置です。それは1つ以上の部品から成り、特定の

人気の比較
タクシーとタクシーの違い

主な違い：「タクシー」と「タクシー」という用語は、どちらもタクシーキャブという用語から派生しています。それらは同義語です。彼らは両方とも言及します非共有の乗車のためにしばしば一人の乗客または乗客の小さいグループによって使用される運転手と一緒に雇うためのタイプの乗り物です。「タクシー」と「タクシー」という用語は本質的に同義語です。どちらも輸送のために借りることができる車を指します。車両はある場所から1つを受け取り、それらを別の場所に移動させます。タクシーとして知られています。「タクシー」と「タクシー」という用語はどちらも「タクシー」という用語から派生しています。旅客は、このサービスに対して固定料金または移動距離に応じて支払う必要があります。ほとんどが個人的に使用されていますが、公共交通機関の一部としても使用されています。タクシーの場合は、固定された場所から乗客を受け取り、別の固定された場所に降ろします。公共タクシーと民間タクシーの種類の組み合わせである共有タクシーと呼ばれるものもあります。シェアリングタクシーまたはシェアタクシーは、時刻表なしで固定または半固定ルートに沿って一群の乗客を連れて行きます。彼らはすべての座席がいっぱいになったときにのみ出発し、グループ全体を決まった場所に落とすか、またはバスサービスのように経路に沿って一人ずつ落としてもよい。地域に

人気の比較
マネーマーケット口座と普通預金口座の違い

主な違い：マネーマーケット口座は、口座内の現金でより良い収益をもたらす、より利回りの高い普通預金口座です。普通預金口座では、銀行は他の人々にローンを提供するためにそのお金を使うことしかできません。マネーマーケット口座では、資金は、トレジャーノート、預金証書、地方債などのマネーマーケット商品に使用されます。その見返りに、彼らはより高い金利を顧客に提供します。節約されたお金は常に銀行と何らかの種類の口座に入ります。アカウントを使用すると、小切手の作成、自動支払いの送信が簡単になります。また、靴下の引き出しや冷蔵庫にお金を家に置いておくよりもはるかに安全です。ユーザーが自分のお金を節約することを可能にする地元の銀行で利用可能なさまざまな異なるアカウントがあります。これらの口座は、銀行が口座のお金で何をすることができるか、そして顧客が受け取る利益を決定します。これらの銀行口座には、普通預金口座、給与口座、当座預金口座、マネーマーケット口座などがあります。マネーマーケット口座と普通預金口座は、人々がお金を預けることができる2種類の口座です。これらのアカウントは、顧客にさまざまなメリットをもたらします。マネーマーケットという用語は、人々が短期の借り入れと貸し出しを行う口座または実際のマネーマーケットを指すことがあります。マネーマーケットは、短期借入金を発行できる金融市場の

人気の比較
AppleとWindowsの違い

主な違い：アップルはグラフィカルユーザインタフェースを中心に設計されています。 Apple Incは、以前はApple Computer Incと呼ばれていました。Appleシステムは、さまざまな種類のオペレーティングシステムに分類されます。Macのコンピュータ、iPodミュージックプレーヤー、iPhoneのスマートフォン、iPadのタブレットコンピュータです。 Windowsは、Microsoftによって開発および販売されている一連のグラフィカルユーザーインターフェイスです。 Windowsシステムは、電話、タブレット、PCなど、さまざまな種類のオペレーティングシステムに分類されます。 AppleとWindowsは2つのオペレーティングシステムです。どちらのコンピュータも同様の機能を提案していますが、どちらのオペレーティングシステムもかなり似ていません。 Apple I、またはApple-1としても遡及的に知られているオリジナルのApple Computerは、1976年にApple Computer Company（現在はApple Inc.）によってリリースされたパーソナルコンピュータです。これらはSteve Wozniakによって設計され、手作りされました。 Wozniakの友人Steve Jobsはコンピュータを売るという考えを持っていました。 Apple私がApple

人気の比較
地表水と地下水の違い

主な違い：地表水とは、湖、池、海など、地球の表面にある水のことです。地下水とは、地面に浸透し貯められた水のことです。地表水と地下水は私たちが飲用、洗濯、調理などの目的のために水を受け取る2つの資源です。地表水は地球の表面にある水です。地理は、地球上で利用可能なすべての水の97％が塩水であるのに対し、3％は淡水であると教えてくれました。この3％の淡水は、私たちが日々の活動に使うものです。ただし、地表水には、池、湖、川、さらには海、小川などに見られる水が含まれます。水が地球から蒸発し、降水に変わり、その後雨の形で戻る水循環表面に水を補給する。地表水は、水の清浄度によって5つの異なるクラスに分類されます。地表水はバクテリア、石油、ガソリンそして他の水の農薬によって汚染されていると考えられています。地下水は、地面に浸透して貯留された水です。浜辺で、あなたがより多くの水を発見するのをより深く掘り下げることに気づいてください、これはそれに似ています。水は地表の真下にある土壌の間隙や、帯水層として知られる石の割れ目の中にあります。帯水層は大量の水を保持することができます、それが一杯になると、それは川や池に逆流します。地下水とは、湖、池、雨水があふれて地面にしみ出た後、近くの水域に流れ込むことです。調査によると、地下水は世界の淡水供給量の約20％を占めています。地下水の

人気の比較

エディターズチョイス

Windows MobileとWindows CEの違い

主な違い： Windows Mobileは、スマートフォンとポケットPCのオペレーティングシステムファミリです。 Windows Mobileは、同社によって廃止され、Windows Mobileの最終バージョンは6.5.5になりました。 Windows CEは、マイクロソフトによる組み込みシステム用のリアルタイムオペレーティングシステムです。 Windows Embedded Compact、Windows Embedded CE、またはWinCEとも呼ばれます。 Windows MobileとWindows CEは、デバイスごとに異なる2種類のオペレーティングシステムです。 Windows Mobileは携帯電話用のオペレーティングシステムのファミリですが、Windows CEは組み込みシステム用のオペレーティングシステムのファミリです。 Windows Mobileは、スマートフォンとポケットPCのオペレーティングシステムファミリです。 Windows Mobileは、スマートフォン用の最新のオペレーティングシステムであるWindows Phoneの前身です。 Windows Mobileは、同社によって廃止され、Windows Mobileの最終バージョンは6.5.5になりました。 Windowsは主にポケットPCで一般的になり、ビジネスマンは毎日の予定を維持したり、予定を追